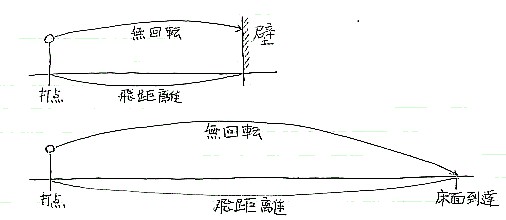
Ⅵ.補足実際のサービスボールの速度について、簡単な測定実験を行なった。コンピュータの軌跡の計算では、初速17 m/s のサーブで18.9 m を1.44秒だから平均すると13.1 m/s 、約4 m/s 小さめに出ている。この差は軌跡の頂点が高くなるほど大きく、飛距離が短くなるほど小さくなると考えられる。実測値を表に示す。

| ボール・サイズ (号) |
到達 | 飛距離 (m) |
サーブとして の速さ |
平均所要時間 (秒) |
平均速度 ( m/s ) |
| 5 | 壁 | 12.3 | 速め | 0.70 | 17.5 |
| 〃 | 〃 | 〃 | 並 | 0.80 | 15.5 |
| 〃 | 〃 | 〃 | 少し抜く | 0.90 | 13.5 |
| 〃 | 〃 | 〃 | 初速最低 | 1.20 | 10.5 |
| 5 | 壁 | 15.2 | 速め | 0.85 | 18.0 |
| 〃 | 〃 | 〃 | 並 | 0.95 | 16.0 |
| 〃 | 〃 | 〃 | 少し抜く | 1.10 | 14.0 |
| 〃 | 〃 | 〃 | 山なり | 1.6 | 9.5 |
| 4 | 床面 | 24 | 少し速め | 1.70 | 14.0 |
| 5 | 壁 | 21.2 | 少し速め | 1.50 | 14.0 |
| 5 | 壁 | 18.3 | 少し速め | 1.30 | 14.0 |
| 5 | 床面 | 24 | 並〜速め | 1.6〜1.4 | 15〜17 |
これより先は、これまで述べてきた現象が実際に起こっている事を、流れの様子を見る事で実証しようとするものである。
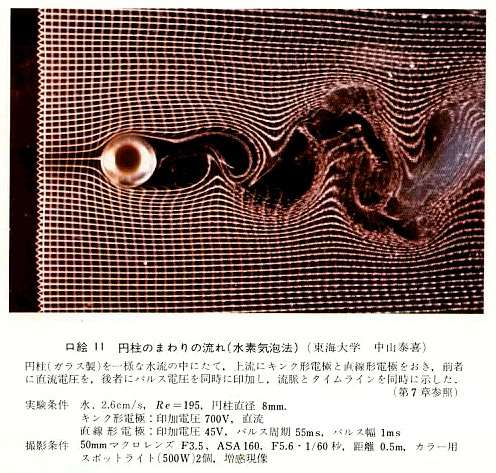
下の写真は、水の流れの中にガラス製の円柱を立て、上流に2種類の電極線に特殊な電圧をかけて網目状の水素気泡を発生させ、円柱まわりの流れの様子を見たものである。後方の流れが大きくかき乱されているのがわかる。なお、写真では円柱の上側と下側からそれぞれ反対まわりの渦が交互に発生しながら後方に流れているが、円柱の場合はこのような渦の列(カルマン渦列と呼ばれる)が発生するのが普通である。よく風の強い日に電線がうなるのを聞くことがあるが、これは円柱後方の空気が渦列によって規則正しく振動するからである。球の場合は振動の方向が複雑になって、このような渦列は発生しにくいようである。
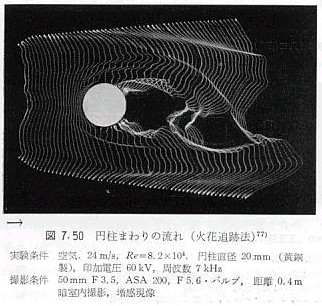 |
雷が落ちる時、続けて光った時に最初の光の通った道筋と全く同じところを通るのを見ることができる。これは、一度雷光が通るとその部分がイオン化されて、電気を通しやすくするからである。この性質を利用して空気の流れを見ることができる。左の写真がそれで、最初の火花でイオン化された空気が円柱の前ではほぼ均一に流れているのに対し、後方では大きく不規則に乱れているのがわかる。 |
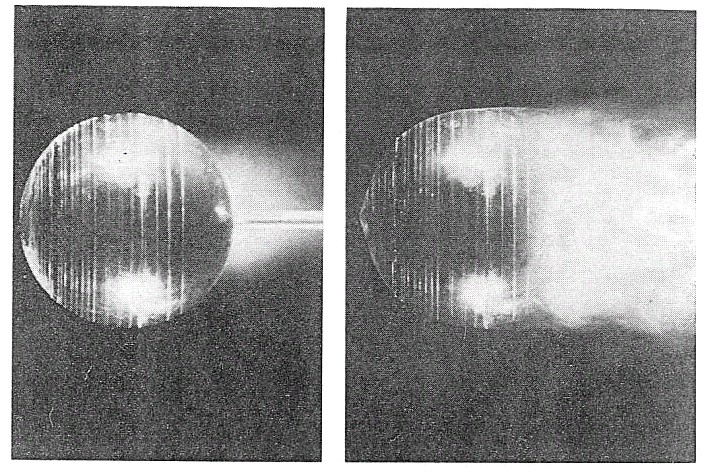
上の写真は臨界レイノルズ数以下の速度での流れ(右)と臨界レイノルズ数を超える速度での流れ(左)を示している。空気に触れると煙を生ずる四塩化チタンを球の先端につけると、流れが球面に沿って流れている部分は煙は薄い層になって流れるのでほとんど見えないが、流れが球面から剥がれると白い煙となって乱れた部分に充満する。臨界レイノルズ数以下では乱れの部分が球の直径より大きく、臨界レイノルズ数以上では直径より小さくなっているのがわかる。
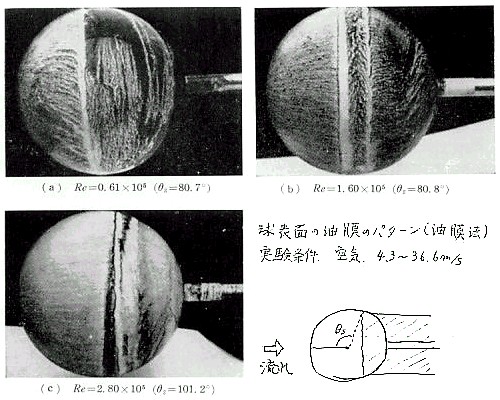
表面上の流れを調べるために、面に油滴をつけて流れにさらすと流れに沿って油も流れ、流れの剥がれるところには油が溜まる。この方法によって球の剥がれ点がレイノルズ数によって移動する事を示したのが、上の写真である。(a)、(b)は臨界レイノルズ数より充分に小さい場合。(c)は臨界レイノルズ数以下だがそれに近い速度の場合。(b)では剥がれ点が2つ見えているが、前方の線が本来の流れの剥がれ点を示し、その後方の線は、その後方から巻き返して来た流れが剥がれている事を示している。また、(b)では剥がれ方は二重でも剥がれの位置は安定しているのに対し、(c)では剥がれ方は更に複雑で剥がれの位置も上と下で一定していないようである。
 |
左の写真は5本の、間隔をおいて立てられた円柱の列に、急に流れを当てた時の流れの様子を示している。5本の円柱を5本の指に見立てて、サーブを打つ手のまわりにこのような乱れが発生しているかもしれない、と考える事もできる。実際に確かめてみなければ何とも言えないが、サーブを打つ瞬間には下図のような渦がボールの後方にできているかもしれない。 |