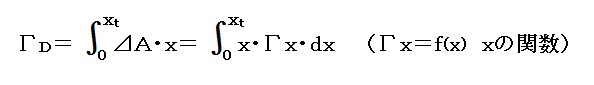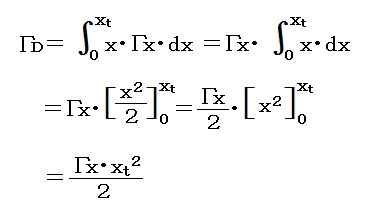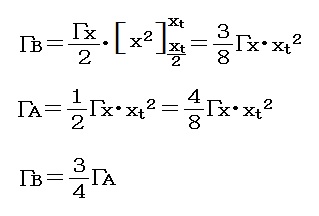実効上反角とは
その主翼の上反角の効果を、翼根から翼端まで一定角とした場合に換算することができれば、さまざまなパターンの上反角の効果を比較できるようになる。この換算された値を「実効上反角」と名付けることを提案する。
なお、後退翼の場合は迎角によって上反角効果が変化するので、質の異なる上反角効果として別に計算して総合的に判断する。ここでは直線翼の上反角を取り扱う。
ΓTotal = ΓDihedral + ΓSwept
ΓDihedral :純粋に上反角による上反角効果。迎角によって変化しない。
ΓSwept :後退角による上反角効果。迎角によって変化する。
以下、ΓDihedral(ΓD)を積分方式で求める。
|
幾何学的基本理論
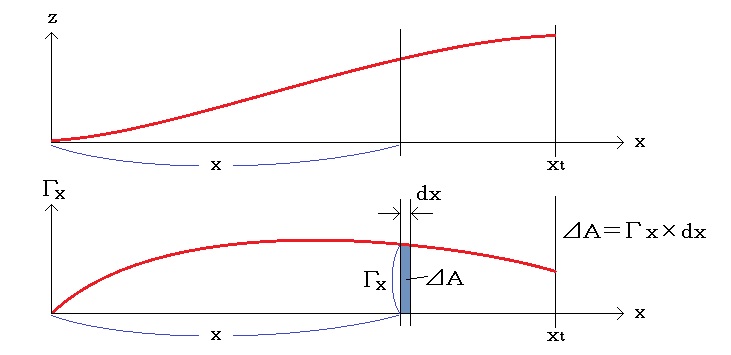
翼根からxの距離にある微小面積ΔAは、上反角効果としてΔA×xの効果がある。(ΔAではない。)翼全体(片翼)としては、
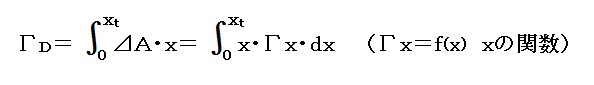
の効果がある。
|
上反角が一定の場合
変換先のΓDは、一定上反角である。一定上反角の場合の”実効上反角”を求めてみる。
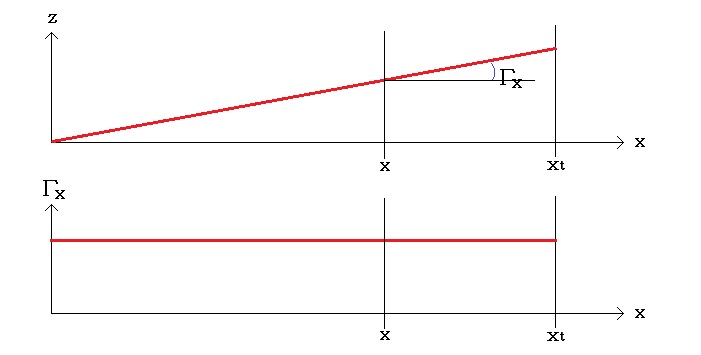
Γxはxに関係なく一定(定数)であるから、
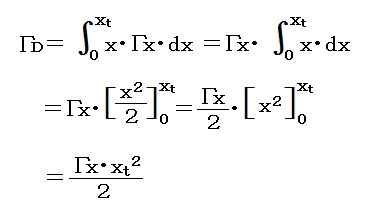
|
比較の実例
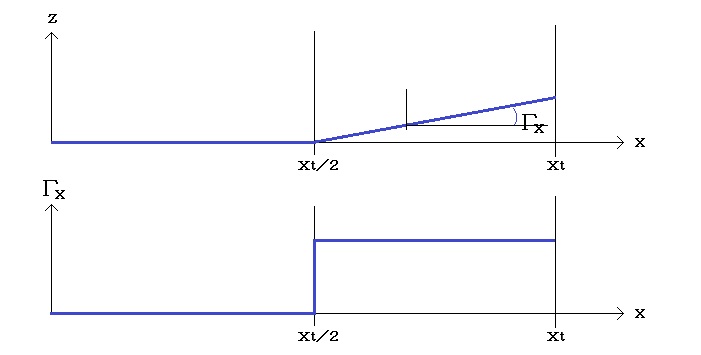
さて、ラジコングライダーのラダー機(エルロンはなく、ラダーをきる事で主翼の上反角効果を利用して機体を傾ける操縦方式)においては、主翼片翼の1/2の位置まで上反角ゼロでそれより外側に上反角をつけると、その翼端の高さになるように翼根から一定の上反角をつけた場合と比べて上反角効果は大きい、という話がある。これを確かめてみよう。
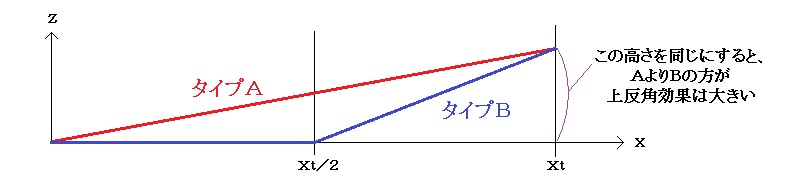
まず、タイプAの上反角Γxと同じ上反角を持つタイプBについて、”実効上反角”を求めてみよう。タイプAの”実効上反角”をΓA、タイプBの”実効上反角”をΓBとして比較ができる。
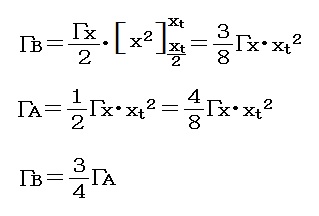
即ち、Γxが同じであれば、タイプBの”実効上反角”はタイプAのそれの3/4である事が分かる。(1/2ではない。)
ところで、確かめたいのは翼端高が同じ場合なので、タイプBの外翼の上反角ΓxBはタイプAの上反角ΓxAより大きい。
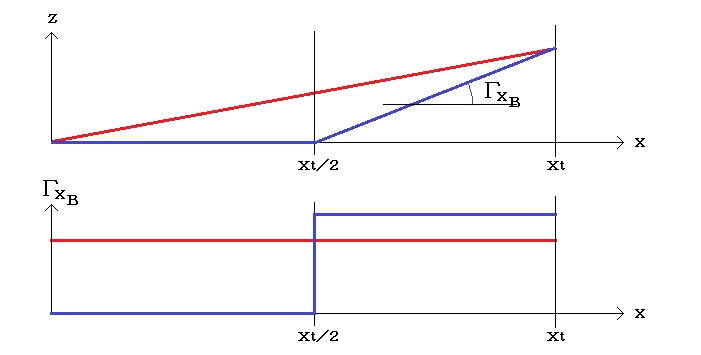
ΓxAとΓxBの比を表す式は複雑になるので、実値で比較する。一般にラダー方式のラジコングライダーの上反角はタイプAの場合、7度が一般的である。これを翼端高の同じタイプBにすると、13.8度になる。
ΓxA:ΓxB=7:13.8
タイプBの”実効上反角”はタイプAの3/4であるから、
ΓxA:ΓxB=7:13.8×3/4=7:10.4≒1:1.5
よって翼端高が同じ場合、タイプBはタイプAの1.5倍の上反角効果がある事が分かり、タイプBはタイプAより上反角効果が大きいという説が証明できた。
では、7度のタイプA翼と同じ上反角効果を持つタイプB翼の外翼の上反角ΓxBはいかほどであろうか。
ΓxB=7度×4/3=9.3度
|